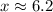Question

Solve for the x round the nearest tenth

Answer 1

x ≈ 6.2

Explanation:

Apply the sine ratio rule where:

`\displaystyle{\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}}`

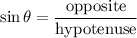
Opposite means a side length of a right triangle that is opposed to the measurement (37 degrees), which is "x".

Hypotenuse is a slant side, or a side length opposed to the right angle, which is 10.3 units.

Substitute θ = 37°, opposite = x and hypotenuse = 10.3, thus:

`\displaystyle{\sin 37^(\circ) = (x)/(10.3)}`

Solve for x:

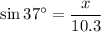
`\displaystyle{\sin 37^(\circ) * 10.3 = (x)/(10.3) * 10.3}\\\\\displaystyle{10.3 \sin 37^(\circ) = x}`

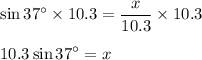
Evaluate 10.3sin37° with your scientific calculator, which results in:

`\displaystyle{6.19869473847... = x}`

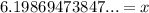
Round to the nearest tenth, hence, the answer is:

`\displaystyle{x \approx 6.2}`

Answer 2

x ≈ 6.2

Explanation:

using the sine ratio in the right triangle

sin37° =
`(opposite)/(hypotenuse)` =
`(AC)/(AB)` =
`(x)/(10.3)` ( multiply both sides by 10.3 )

10.3 × sin37° = x , then

x ≈ 6.2 ( to the nearest tenth )