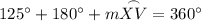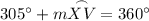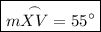Question

NO LINKS!! URGENT HELP PLEASE!!

Find each indicated measure ​

Answer 1

`\text{b.} \quad m\overset{\frown}{XW}=160^(\circ)`

`\text{d.} \quad m\overset{\frown}{XV}=55^(\circ)`

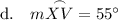
Explanation:

An inscribed angle is the angle formed (vertex) when two chords meet at one point on a circle.

An intercepted arc is the arc that is between the endpoints of the chords that form the inscribed angle.

`\hrulefill`

Part b

From inspection of the given circle:

• The inscribed angle is m∠WRX = 80°
• The intercepted arc is arc XW.

According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc. Therefore:

`m \angle WRX = (1)/(2)\overset{\frown}{XW}`

`80^(\circ)= (1)/(2)\overset{\frown}{XW}`

`\boxed{m\overset{\frown}{XW}=160^(\circ)}`

`\hrulefill`

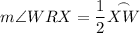
Part d

From inspection of the given circle:

• The inscribed angle is m∠WVX = 90°
• The intercepted arc is arc WX.

According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc. Therefore:

`m \angle WVX= (1)/(2)\overset{\frown}{WX}`

`90^(\circ)= (1)/(2)\overset{\frown}{WX}`

`m\overset{\frown}{WX}=180^(\circ)`

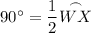
The sum of the measures of the arcs in a circle is 360°.

`m\overset{\frown}{VW}+m\overset{\frown}{WX}+m\overset{\frown}{XV}=360^(\circ)`

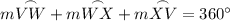
Therefore, so find the measure of arc XV, substitute the found measures of arcs VW and WX, and solve for arc XV:

`125^(\circ)+180^(\circ)+m\overset{\frown}{XV}=360^(\circ)`

`305^(\circ)+m\overset{\frown}{XV}=360^(\circ)`

`\boxed{m\overset{\frown}{XV}=55^(\circ)}`

Answer 2

b. 160°

d. 55°

Explanation:

The Inscribed Angle Theorem states that an inscribed angle is half of the central angle that subtends the same arc.

In other words, if an angle is inscribed in a circle and it intercepts an arc, then the measure of the inscribed angle is equal to half the measure of the central angle that also intersects that arc.

For question:

b.

By using above theorem:

m arc XW=2* m arc XYW

m arc XW= 2*80=160°

d.

m arc WV=125°

The Inscribed Angle Diameter Right Angle Theorem states that any angle inscribed in a circle that intercepts a diameter is a right angle.

By using this theorem:

m arc WV+m arc XV =180°

Now

m arc XV =180°-m arc WV

m arc XV=180°-125°

n arc XV=55°