A certain cubic polynomial has a leading coefficient of 1 and zeros at 0, 1, and 2. What is the equation of the polynomial in standard form?

Question

asked Sep 17, 2024 108k views

1 Answer

Dominik Weber · Answer 1 · 2024-09-23T02:42:31+0000

Certainly! Here's the solution to find the equation of the cubic polynomial with zeros at 0, 1, and 2:

Since the zeros of the polynomial are 0, 1, and 2, we can express the polynomial in factored form as:

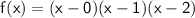
$\sf f(x) = (x - 0)(x - 1)(x - 2) \\$

Simplifying the expression, we get:

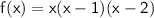
$\sf f(x) = x(x - 1)(x - 2) \\$

Expanding the product, we have:

$\sf f(x) = (x^2 - x)(x - 2) \\$

Using the distributive property, we can further simplify:

$\sf f(x) = (x^3 - 2x^2 - x^2 + 2x) \\$

Combining like terms, we get:

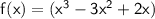
$\sf f(x) = (x^3 - 3x^2 + 2x) \\$

Therefore, the equation of the cubic polynomial with leading coefficient 1 and zeros at 0, 1, and 2, in standard form, is:

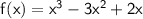
$\sf f(x) = x^3 - 3x^2 + 2x \\$

$\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}$

♥️
$\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}$