Find $ f $ such that $ f^{\prime}(x)=\frac{8}{\sqrt{x}}, f(16)=74 $ \[ f(x)= \]

Question

asked Oct 9, 2024 105k views

1 Answer

James Alexander · Answer 1 · 2024-10-15T07:13:47+0000

To find f(x) such that
$\sf\:f'(x) = (8)/(√(x)) \\$ and f(16) = 74 , we can integrate f'(x) to find f(x) .

Using the power rule of integration, we have:

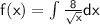
$\sf f(x) = \int (8)/(√(x)) dx \\$

Applying the power rule of integration, we can rewrite the integral as:

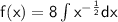
$\sf f(x) = 8 \int x^{-(1)/(2)} dx \\$

Integrating, we get:

$\sf f(x) = 8 \cdot 2x^{(1)/(2)} + C \\$

Simplifying, we have:

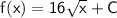
$\sf f(x) = 16√(x) + C \\$

To find the value of C , we use the given condition f(16) = 74 . Substituting x = 16 into the equation, we get:

$\sf 74 = 16√(16) + C \\$

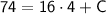
$\sf 74 = 16 \cdot 4 + C \\$

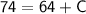
$\sf 74 = 64 + C \\$

Solving for C we have:

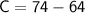
$\sf C = 74 - 64 \\$

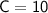
$\sf C = 10 \\$

Therefore, the function f(x) is given by:

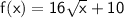
$\sf f(x) = 16√(x) + 10 \\$

I hope this helps! Let me know if you have any further questions.