To solve the equation
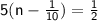 for
for
 , we can follow these steps:
, we can follow these steps:
Step 1: Distribute the 5 on the left side:
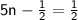
Step 2: Add
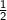 to both sides of the equation:
to both sides of the equation:
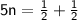

Step 3: Divide both sides of the equation by 5 to isolate
 :
:
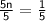

Therefore, the solution to the equation
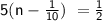 is
is
 , which corresponds to option (d).
, which corresponds to option (d).
♥️