The value of the car in the year 2004, assuming it continues to depreciate at the same annual percentage rate, would be $10,150 when rounded to the nearest $50.
Based on the information provided:
- The car was valued at $29,000 in 1991.
- The value depreciated to $14,000 by the year 2000.
We have already calculated the annual rate of change as:
![\[ r = -0.0777 \]](https://img.qammunity.org/2024/formulas/mathematics/college/4qddbfg4cygzqobr8syfw5mgr9t9c0etw4.png) (or -7.77% when expressed as a percentage)
(or -7.77% when expressed as a percentage)
Now, for part C, we want to calculate the value of the car in the year 2004, assuming the car continues to depreciate at the same annual percentage rate.
Since 4 years have passed from 2000 to 2004, we will apply the annual rate of decrease four times to the value of the car in the year 2000.
The formula for depreciation is:
![\[ \text{Future Value} = \text{Present Value} * (1 + r)^n \]](https://img.qammunity.org/2024/formulas/mathematics/college/rkt5oco0bagw01tgi20e5ephoaupn0b7sp.png)
Where:
-
 is the value we want to find for the year 2004.
is the value we want to find for the year 2004.
-
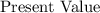 is the value of the car in the year 2000, which is $14,000.
is the value of the car in the year 2000, which is $14,000.
-
 is the annual rate of decrease, which is -0.0777.
is the annual rate of decrease, which is -0.0777.
-
 is the number of years, which is 4.
is the number of years, which is 4.
Let's calculate the future value and then round it to the nearest 50 dollars.
The value of the car in the year 2004, assuming it continues to depreciate at the same annual percentage rate, would be $10,150 when rounded to the nearest $50.