Comparing these points with the given options, we find that option B.
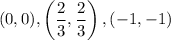 is the correct answer.
is the correct answer.
To determine which vertices form a triangle using the given equations, we can solve the system of equations. Let's start by solving the first two equations:
Equation 1: x + y = 0
Equation 2: x - y = 0
To eliminate y, we can add the two equations together:
(x + y) + (x - y) = 0 + 0
2x = 0
Dividing both sides by 2, we get:
x = 0
Substituting x = 0 into Equation 1, we find:
0 + y = 0
y = 0
So the first two equations give us the point (0, 0).
Now let's solve the second and third equations:
Equation 2: x - y = 0
Equation 3: 2x + y = 1
To eliminate y, we can multiply Equation 2 by 2 and add it to Equation 3:
2(x - y) + (2x + y) = 2(0) + 1
2x - 2y + 2x + y = 1
4x - y = 1
Rearranging the equation, we have:
4x = 1 + y
4x = y + 1
Substituting x = 0, we find:
0 = y + 1
This implies that y = -1. So the second and third equations give us the point (0, -1).
Finally, let's solve the first and third equations:
Equation 1: x + y = 0
Equation 3: 2x + y = 1
To eliminate y, we can multiply Equation 1 by 2 and subtract it from Equation 3:
2(x + y) - (2x + y) = 2(0) - 1
2x + 2y - 2x - y = -1
y = -1
Substituting y = -1 into Equation 1, we find:
x + (-1) = 0
x - 1 = 0
x = 1
So the first and third equations give us the point (1, -1).
Therefore, the vertices of the triangle formed by the three lines are (0, 0), (0, -1), and (1, -1).