Question

Use this definition with right endpoints to find an expression for the area under the graph of f as a limit. Do not evaluate the limit. f(x) = x2ex, 0 ≤ x ≤ 5 A

A = lim n → [infinity]
n i = 1

Answer 1

The area under the graph of f is
`\(A = \lim_(n\rightarrow\infty)\sum_(i=1)^(n)\left((5i)/(n)\right)^2e^{(5i)/(n)}\left((5)/(n)\right)\)`.

Divide the interval [0, 5] into n subintervals of equal length.

The length of each subinterval is
`\(\Delta x = (5-0)/(n) = (5)/(n)\)`.

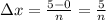The right endpoint of the
`\(i\)-th subinterval is \(x_i = 0 + i\Delta x = 0 + i\left((5)/(n)\right) = (5i)/(n)\)`.

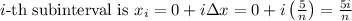The function value at each right endpoint is
`\(f(x_i) = \left((5i)/(n)\right)^2e^{(5i)/(n)}\)`.

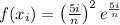Multiply the function value at each right endpoint by the length of the subinterval to find the area of the rectangle above each subinterval.

The area of the rectangle above the
`\(i\)-th subinterval is \(f(x_i)\Delta x = \left((5i)/(n)\right)^2e^{(5i)/(n)}\left((5)/(n)\right)\)`.

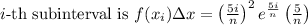Sum the areas of all rectangles to approximate the total area under the graph of f over the interval [0, 5].

The sum of the areas of all rectangles is
`\(\sum_(i=1)^(n)\left((5i)/(n)\right)^2e^{(5i)/(n)}\left((5)/(n)\right)\)`.

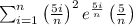Question: