Question

4. (x,y) → (x-3,4-y) is an example of a transformation

called a glide reflection. Complete the table using the
rule.
(0.2) og (0.0) mont
Does this glide reflection produce a triangle congruent to
the original? odigrals
grofs siGnE IT E
(0.8) of (0,0) mail inemgs2
beeb ortignols sislaris 7 A
(,0) 0 (0,0) montinangg
al baina eft gnols eslarist 2
(E+E+
input
(1, 1)
(6, 1)
(3,5)
output
(-2,3)
(E-(.*)-(x) =
(6+x,x) - (x)

Answer 1

(3, 3)

(0, -1)

Yes, the glide reflection produces a triangle congruent to the original.

Explanation:

A glide reflection is a type of transformation that combines a translation and a reflection.

Given glide reflection rule:

`\boxed{(x,y) \rightarrow (x-3,4-y)}`

To complete the table using the given transformation rule, we can apply the rule to each input point.

`(1, 1) \rightarrow (1-3,4-1)=(-2,3)`

`(6, 1) \rightarrow (6-3,4-1)=(3,3)`

`(3,5) \rightarrow (3-3,4-5)=(0,-1)`

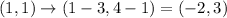
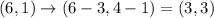
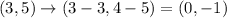
Therefore, the completed table is:

`\begin{array}c\cline{1-2}\vphantom{\frac12} \sf I\:\!nput & \sf O\:\!utput\\\cline{1-2}\vphantom{\frac12} (1, 1) & (-2, 3)\\\cline{1-2}\vphantom{\frac12} (6, 1) & (3, 3)\\\cline{1-2}\vphantom{\frac12} (3, 5) & (0, -1)\\\cline{1-2}\end{array}`

The glide reflection is a series of transformations:

• x - 3 is a translation of 3 units left.
• 4 - y is a reflection in the x-axis, followed by a translation of 4 units up.

Therefore, the original triangle has been translated, reflected and translated.

A translation moves the figure to a new location. Every point of the figure is moved the same distance in the same direction, so a translation preserves shape and size. Therefore, the resulting figure will be congruent to the original figure.

A reflection creates a mirror image of the original figure in a line of reflection. Reflections preserve shape and size, so if a figure is reflected, the resulting figure will be congruent to the original.

Therefore, since translations and reflections preserve shape and size, the combination of these transformations results in a congruent figure.

So the glide reflection produces a triangle congruent to the original.