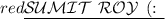To determine the length of the hypotenuse in a 30-60-90 triangle, we can use the ratios derived from the special properties of this type of triangle.
In a 30-60-90 triangle, the ratios of the sides are as follows:
The side opposite the 30-degree angle is half the length of the hypotenuse.
The side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle.
The hypotenuse is twice the length of the side opposite the 30-degree angle.
In the given options, the length of the side opposite the 30-degree angle is 12. Therefore, the length of the hypotenuse, which is twice the length of the side opposite the 30-degree angle, would be:
Hypotenuse = 2 * 12 = 24
So, the length of the hypotenuse in the 30-60-90 triangle is 24.

♥️