Question

HELP PLEASEEEE!!!!! I WILL MARK!!!!!!

If y = 3x2 − 9, what is its inverse?

A. inverse of y is equal to negative square root of the quantity x plus 9 over 3 end quantity such that x is greater than or equal to negative 9
B. inverse of y is equal to negative square root of the quantity x plus 9 over 3 end quantity such that x is less than or equal to negative 9
C. inverse of y is equal to negative square root of the quantity x over 3 end quantity plus 9 such that x is less than or equal to 0
D. inverse of y is equal to negative square root of the quantity x over 3 end quantity plus 9 such that x is greater than or equal to 0

Answer 1

A

Explanation:

Given quadratic function:

`y=3x^2 - 9, \qquad x \leq 0`

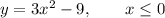
The domain of the given function is restricted to values of x less than or equal to zero. Therefore:

• The domain is x ≤ 0.

As 3x² ≥ 0, then range of the given function is restricted to values of y greater than or equal to -9.

• The range is x ≥ -9.

`\hrulefill`

To find the inverse of the given function, first interchange the x and y variables:

`x = 3y^2 - 9`

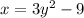
Now, solve the equation for y:

`\begin{aligned}x& = 3y^2 - 9\\\\x+9&=3y^2\\\\(x+9)/(3)&=y^2\\y&=\pm \sqrt{(x+9)/(3)}\end{aligned}`

The range of the inverse function is the domain of the original function.

As the domain of the original function is restricted to x ≤ 0, then the range of the inverse function is restricted to y ≤ 0.

Therefore, the inverse function is the negative square root:

`f^(-1)(x)=-\sqrt{(x+9)/(3)}`

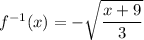
The domain of the inverse function is the range of the original function.

As the range of the original function is restricted to y ≥ -9, then the domain of the inverse function is restricted to x ≥ -9.

`\boxed{f^(-1)(x)=-\sqrt{(x+9)/(3)}\qquad x \geq -9}`

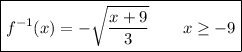
So the correct statement is:

• A) The inverse of y is equal to negative square root of the quantity x plus 9 over 3 end quantity such that x is greater than or equal to negative 9.