Question

A quality engineer samples 100 steel rods made on mill A and 150 rods made on mill B. Of the rods from mill A, 88 meet specifications, and of the rods from mill B, 135 meet specifications. Estimate the proportion of rods from mill A that meet specifications, and find the uncertainty in the estimate. Estimate the proportion of rods from mill B that meet specifications, and find the uncertainty in the estimate. Estimate the difference between the proportions, and find the uncertainty in the estimate

Answer 1

The proportions of steel rods meeting specifications from mills A and B are estimated as 88% and 90% respectively. The uncertainties in these estimates are found using the standard error for proportions. The difference between the proportions is calculated, and its uncertainty is found by combining the standard errors of both estimates.

Step-by-step explanation:

The student is asking about estimating proportions of steel rods meeting specifications from two different mills (A and B), and the uncertainty associated with these estimates. Additionally, there is a need to estimate the difference between the proportions and the uncertainty of this difference.

To estimate the proportion of steel rods from mill A that meet specifications, we use the formula: Proportion = Number meeting specifications / Total number sampled. Thus for mill A, Proportion_A = 88/100 = 0.88 or 88%. To find the uncertainty in this estimate, we use the standard error of a proportion, which is calculated as SE = sqrt[Proportion_A * (1 - Proportion_A) / n], where n is the sample size. For mill A, SE_A = sqrt[0.88 * (1 - 0.88) / 100] = 0.032.

Similarly, for mill B, the Proportion_B = 135/150 = 0.9 or 90%, and the uncertainty, SE_B, is calculated as SE_B = sqrt[0.9 * (1 - 0.9) / 150] = 0.024.

To estimate the difference between the proportions, we subtract Proportion_B from Proportion_A. Difference = Proportion_A - Proportion_B. The uncertainty in the estimate of the difference is found using the formula for combining standard errors: SE_difference = sqrt(SE_A^2 + SE_B^2).

The concept of estimating proportions and their uncertainties relates to creating confidence intervals for population proportions, which is an important aspect of inferential statistics.

Answer 2

1. The estimated proportion of rods from mill A that meet specifications is 0.88, with an uncertainty of approximately 0.032.

2. The estimated proportion of rods from mill B that meet specifications is 0.9, with an uncertainty of approximately 0.0245.

3. The estimated difference between the proportions is 0.02, with an uncertainty (standard error) of approximately 0.039.

How to estimate the proportion

To estimate the proportion of rods from mill A that meet specifications, divide the number of rods from mill A that meet specifications (88) by the total number of rods from mill A sampled (100):

Thus;

Proportion of rods from mill A that meet specifications

= 88/100

= 0.88

To find the uncertainty in the estimate, use the formula for the standard error of a proportion:

Standard error =
`\sqrt`((p * (1 - p)) / n)

where p is the estimated proportion and n is the sample size.

Standard error for mill A =
`\sqrt`((0.88 * (1 - 0.88)) / 100) ≈ 0.032

Therefore, the estimated proportion of rods from mill A that meet specifications is 0.88, with an uncertainty (standard error) of approximately 0.032.

Similarly, to estimate the proportion of rods from mill B that meet specifications, divide the number of rods from mill B that meet specifications (135) by the total number of rods from mill B sampled (150):

Proportion of rods from mill B that meet specifications

= 135/150

= 0.9

The uncertainty in the estimate can be calculated using the same formula:

Standard error for mill B =
`\sqrt`((0.9 * (1 - 0.9)) / 150) ≈ 0.0245

Therefore, the estimated proportion of rods from mill B that meet specifications is 0.9, with an uncertainty (standard error) of approximately 0.0245.

To estimate the difference between the proportions, we subtract the proportion of rods from mill B that meet specifications from the proportion of rods from mill A that meet specifications:

Difference in proportions = 0.9 - 0.88 = 0.02

The uncertainty in the difference can be calculated using the formula for the standard error of the difference between two proportions:

Standard error of difference =
`\sqrt((se_A)^2 + (se_B)^2`)

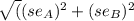Standard error of difference =
`\sqrt((0.032)^2 + (0.023)^2)`

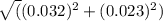
≈ 0.039

Therefore, the estimated difference between the proportions is 0.02, with an uncertainty (standard error) of approximately 0.039.