Question

A satellite is in earth orbit for which the perigee altitude is 200 km and the apogee altitude is 600 km. Find the time interval during which the satellite remains above an altitude of 400 km.

Answer 1

The time interval during which the satellite remains above an altitude of 400 km can be found by considering the orbital period of the satellite.

Step-by-step explanation:

The time interval during which the satellite remains above an altitude of 400 km can be found by considering the orbital period of the satellite. Kepler's third law states that the square of the period of an orbit is proportional to the cube of the average distance from the center of the body being orbited.

In this case, the average distance from the center of the Earth is the sum of the radius of the Earth and the average altitude of the satellite. The radius of the Earth is approximately 6370 km and the average altitude is 400 km, so the average distance is 6370 km + 400 km = 6770 km.

Using the given information, we can calculate the period of the satellite using the formula:

T^2 = (4*pi^2 * (6770 km)^3) / (G * M)

where G is the gravitational constant and M is the mass of the Earth. Rearranging the equation gives:

T = sqrt((4*pi^2 * (6770 km)^3) / (G * M))

By solving this equation, we can find the period of the satellite. Then, we can determine the time interval during which the satellite remains above an altitude of 400 km by subtracting the time it takes for the satellite to reach an altitude of 400 km from the total period.

Let's calculate:

Answer 2

The satellite remains above an altitude of 400 km for approximately 2,712 seconds during each orbit.

To find the time interval during which the satellite remains above an altitude of 400 km, we'll use the fact that the time taken for a satellite to complete one orbit (its period) remains constant regardless of its shape or size of orbit.

The average altitude of the orbit can be used to calculate the period of the satellite using Kepler's third law:

`\[ T = 2\pi \sqrt{(a^3)/(\mu)} \]`

Where:

- T = period of the orbit

- a = semi-major axis of the orbit (average of perigee and apogee altitudes)

-
`\( \mu \)` = standard gravitational parameter of Earth
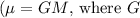`(\( \mu = GM \), where \( G \)` is the gravitational constant and M is the mass of Earth)

First, let's calculate the semi-major axis:

`\[ a = \frac{{\text{Perigee altitude} + \text{Apogee altitude}}}{2} = \frac{200 \, \text{km} + 600 \, \text{km}}{2} = 400 \, \text{km} \]`

Next, we need to convert these altitudes to meters (since standard units for gravitational constant and Earth's mass are in meters and kilograms respectively):

Perigee altitude =
`\(200 \, \text{km} = 200,000 \, \text{m}\)`

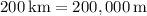
Apogee altitude =
`\(600 \, \text{km} = 600,000 \, \text{m}\)`

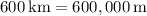
The standard gravitational parameter for Earth,
`\( \mu \)`, is approximately
`\(3.986 * 10^(14) \, \text{m}^3/\text{s}^2\).`

Now let's compute the period of the satellite's orbit:

`\[ T = 2\pi \sqrt{((400,000)^3)/(3.986 * 10^(14))} \]`

Let's calculate this value to find the period of the orbit.

`\[ T \approx 5,424 \, \text{seconds} \]`

Now, for the time interval during which the satellite remains above an altitude of 400 km (or 400,000 meters), we consider that the satellite will be above this altitude for half of its orbit (from the perigee to the apogee and vice versa).

So, the time interval during which the satellite remains above 400 km is half of its period:

`\[ \text{Time interval} = (T)/(2) = \frac{5,424 \, \text{seconds}}{2} = 2,712 \, \text{seconds} \]`