Answer:
The function will have 2 zeroes.
Explanation:
To find how many zeroes a quadratic function would have, we would have to look at its discriminant.
The discriminant (written using the capital greek letter Delta) of a quadratic function is defined like so:
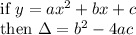
If the discriminant of a function is:
- Greater than 0, then it will have two zeroes.
- Equal to 0, then it will have one zero.
- Less than 0, then it will not have any zeroes.
Since we're given that
 and
and
 , then
, then
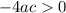 , as multiplying two negative numbers results in a positive number.
, as multiplying two negative numbers results in a positive number.
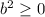 for all b, as any number times itself is positive/zero (for the same reason that -4ac is positive).
for all b, as any number times itself is positive/zero (for the same reason that -4ac is positive).
Therefore,
 for all a > 0 and c < 0.
for all a > 0 and c < 0.
Meaning that the function will have two zeroes.