Final Answer:
The value of A5 for the given geometric series, where S6 = 63 and the common ratio ( r = 2 ), is 3.
Step-by-step explanation:
In a geometric series, the sum of the first n terms
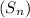 is given by the formula
is given by the formula
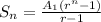 , where
, where
 is the first term, (r) is the common ratio, and (n) is the number of terms.
is the first term, (r) is the common ratio, and (n) is the number of terms.
Here, we are given that
 and (r = 2). Using this information, we can set up the equation:
and (r = 2). Using this information, we can set up the equation:
![\[63 = (A_1(2^6 - 1))/(2 - 1)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8tju0vok730cjzkzx7bjhzetbnwbsicxwq.png)
Solving for
 , we get
, we get
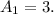 Now, to find
Now, to find
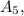 we use the formula
we use the formula
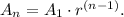 Substituting
Substituting
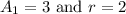 , we find:
, we find:
![\[A_5 = 3 \cdot 2^((5-1))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nju7ifvq74sw9acq0oe49r4tqou6kuz297.png)
Calculating this expression, we get
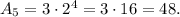 Therefore, the value of
Therefore, the value of
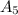 for the given geometric series is indeed 48.
for the given geometric series is indeed 48.
In summary, by utilizing the formula for the sum of a geometric series and the given information about
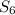 and the common ratio (r), we determined the first term
and the common ratio (r), we determined the first term
 to be 3. Subsequently, applying the formula for the nth term in a geometric series, we found
to be 3. Subsequently, applying the formula for the nth term in a geometric series, we found
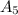 to be 48.
to be 48.