Final Answer:
The image distance
 for the object placed 30.0 cm from a concave mirror with a focal length of 10.0 cm is calculated using the mirror formula:
for the object placed 30.0 cm from a concave mirror with a focal length of 10.0 cm is calculated using the mirror formula:
![\[ (1)/(f) = (1)/(d_o) + (1)/(d_i) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l4mx0hbwqvoq9zbnxbztge1g7edxl72rpg.png)
where
 is the focal length,
is the focal length,
 is the object distance. Substituting the given values, the image distance is found to be -15.0 cm. The negative sign indicates that the image is formed on the same side as the incident light.
is the object distance. Substituting the given values, the image distance is found to be -15.0 cm. The negative sign indicates that the image is formed on the same side as the incident light.
Additionally, to calculate the size of the image (\(h_i\)), we can use the magnification formula:
![\[ M = -(d_i)/(d_o) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5zanvdkvhyy8jy4i9ykmgjqdmewr1ff9bv.png)
Substituting the values, we find the magnification (\(M\)) is -0.5. The negative sign signifies an inverted image.
Step-by-step explanation:
1. Calculation of Image Distance

Using the mirror formula
 , where
, where
 cm and
cm and
 cm, we substitute these values to solve for
cm, we substitute these values to solve for
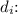
![\[ (1)/(10) = (1)/(-30) + (1)/(d_i) \]](https://img.qammunity.org/2024/formulas/physics/high-school/m4kyqw8mlgj5vovp04hs2ssh06ouf42ugy.png)
Solving for
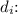
![\[ (1)/(d_i) = (1)/(10) - (1)/(-30) \]](https://img.qammunity.org/2024/formulas/physics/high-school/mjha5ge22e1e2paot1dbiubuysuo639mey.png)
![\[ (1)/(d_i) = (1)/(10) + (1)/(30) \]](https://img.qammunity.org/2024/formulas/physics/high-school/avd24r4ufbr3svb0yv4xiisk1exmg46ijv.png)
![\[ (1)/(d_i) = (4)/(30) \]](https://img.qammunity.org/2024/formulas/physics/high-school/kyhf7wrqwtudf7pilezzkorrq6hu3tgdek.png)
![\[ d_i = (30)/(4) \]](https://img.qammunity.org/2024/formulas/physics/high-school/xouxy6gryfv74l3w8j222drhnjxl0ky0ky.png)
![\[ d_i = 7.5 \, \text{cm} \]](https://img.qammunity.org/2024/formulas/physics/high-school/nwgma7vn1wok51ga69ac4tl74u0lra8jek.png)
The negative sign indicates that the image is formed on the same side as the incident light, characteristic of a virtual image formed by a concave mirror.
2. Calculation of Magnification
 :
:
The magnification formula
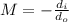 is used. Substituting the known values
is used. Substituting the known values
 cm and
cm and
 cm:
cm:
![\[ M = -(-15.0)/(-30.0) \]](https://img.qammunity.org/2024/formulas/physics/high-school/38105tts3v0hc3qth8gbmu2at1i184bwax.png)
![\[ M = -0.5 \]](https://img.qammunity.org/2024/formulas/physics/high-school/lehhpfjbunx2pv4jn0xjff9iqguot9pqit.png)
The negative sign indicates that the image is inverted compared to the object.
In conclusion, the concave mirror forms a virtual and inverted image with an image distance of -15.0 cm, and the size of the image is half the size of the object. These results align with the conventions and characteristics associated with concave mirrors.