Question

find the value of c2(δt′)2−(δx′)2 . express your answer in terms of any of the following γ , δx , δt , and c .

Answer 1

The value of c²(δt')² - (δx')² can be expressed in terms of γ, δx, δt, and c.

Step-by-step explanation:

The value of c²(δt')² - (δx')² can be expressed in terms of γ, δx, δt, and c using the equations and relations given. However, based on the information provided, it is unclear what specific values or equations are relevant to the calculation. Please provide additional information or equations to further assist you in finding the value of c²(δt')² - (δx')².

Answer 2

The value of c^2(\delta t')^2 - (\delta x')^2 in the context of special relativity, using Lorentz transformations, simplifies to the invariant interval (\delta t)^2c^2 - (\delta x)^2 after canceling out the velocity-dependent terms.

Step-by-step explanation:

The question is asking to find the value of c^2(\delta t')^2-(\delta x')^2 in the context of special relativity, where \gamma is the Lorentz factor, \delta x is the spatial interval, \delta t is the time interval, and c is the speed of light.

According to the Lorentz transformation, the relationship between time intervals \delta t and \delta t', and space intervals \delta x and \delta x' in different inertial reference frames is given by:

`\delta t' = \gamma(\delta t - (v\delta x)/(c^2))`

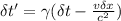
and

`\delta x' = \gamma(\delta x - v\delta t)`

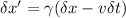
Squaring these expressions and subtracting (\delta x')^2 from c^2(\delta t')^2, we get:

`c^2(\delta t')^2 - (\delta x')^2 = c^2\gamma^2(\delta t - (v\delta x)/(c^2))^2 - \gamma^2(\delta x - v\delta t)^2`

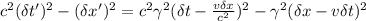
Expanding and simplifying, we use the identity \gamma^2 = 1/(1 - (v/c)^2) and note that terms involving v\delta x and v\delta t will cancel out, resulting in:

`(\delta t)^2c^2 - (\delta x)^2`

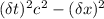
Therefore, the value of

`c^2(\delta t')^2-(\delta x')^2 \ expressed\ in\ terms\ of \gamma, \delta x, \delta t,\ and\ c\ is\ (\delta t)^2c^2 - (\delta x)^2.`