Question

Question and answers are in the picture but this is worth 100 bainly points. I need help asap

Answer 1

Answer: D

Explanation:

Here's a trick for these types of questions.
`sin^2+cos^2=1`

So, 5/6*5/6=25/36.

1-25/36=11/36

11/36 square root is:

`√(11) /√(36)`

The square root of 36=6

So the answer is B or D.

As an explanation, tan=sin*cos, and (square root of 11)/6*5/6=5*(square root of 11)/6,

The answer is D.

Answer 2

`\textsf{d)}\quad \cos\theta=\pm (√(11))/(6)\: ;\quad \tan \theta=\pm(5√(11))/(11)`

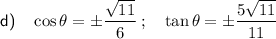
Explanation:

To calculate the exact values of cos θ and tan θ, given that sin θ = 5/6, we can use first use the Pythagorean trigonometric identity to find cos θ.

`\boxed{\begin{array}{c}\underline{\textsf{Pythagorean trigonometric identity}}\\\\\sin^2\theta+\cos^2\theta=1\\\end{array}}`

Substitute the given value of sin θ = 5/6 into the identity and solve for cos θ:

`\begin{aligned}\left((5)/(6)\right)^2+\cos^2\theta&=1\\\\\cos^2\theta&=1-\left((5)/(6)\right)^2\\\\\cos^2\theta&=(36)/(36)-(25)/(36)\\\\\cos^2\theta&=(11)/(36)\\\\√(\cos^2\theta)&=\sqrt{(11)/(36)}\\\\\cos\theta&=\pm (√(11))/(6)\end{aligned}`

To find the value of tan θ, we can use the tangent trigonometric ratio identity:

`\boxed{\begin{array}{c}\underline{\textsf{Tangent trigonometric ratio identity}}\\\\\tan \theta=(\sin \theta)/(\cos \theta)\end{array}}`

Substitute the given value of sin θ = 5/6 and the found value of cos θ into the identity:

`\begin{aligned}\tan \theta&=((5)/(6))/(\pm(√(11))/(6))\\\\\tan \theta&=\pm(5)/(√(11))\\\\\tan \theta&=\pm(5\cdot √(11))/(√(11)\cdot √(11))\\\\\tan \theta&=\pm(5√(11))/(11)\\\\\end{aligned}`

Therefore, if sin θ = 5/6, the values of cos θ and tan θ are:

`\large\boxed{\boxed{\cos\theta=\pm (√(11))/(6)\:;\quad \tan \theta=\pm(5√(11))/(11)}}`