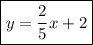Question

..................................................................

Answer 1

`\mathrm{y=(2)/(5)x+2}`

Explanation:

`\mathrm{Here,\ we\ see\ that\ the\ line\ passes\ through\ (-5,0)\ and\ (0,2).}\\\mathrm{So\ the\ equation\ of\ line\ is:}\\\\\mathrm{y-0=(2-0)/(0-(-5))(x-(-5))}\\\mathrm{or,\ y=(2)/(5)(x+5)}\\\mathrm{or,\ 5y=2x+10}\\\mathrm{or,\ y=(2)/(5)x+2}`

Alternative method:

`\mathrm{Here,}\\\mathrm{x-intercept(a)=-5}\\\mathrm{y-intercept(b)=2}\\\mathrm{Now,}\\\mathrm{Equation\ of\ the\ line\ is:}\\\mathrm{(x)/(a)+(y)/(b)=1}\\\\\mathrm{or,\ (x)/(-5)+(y)/(2)=1}\\\\\mathrm{or,\ (2x-5y)/(-10)=1}\\\\\mathrm{or,\ 2x-5y=-10}\\\mathrm{or,\ 5y=2x+10 }\\\\\mathrm{or,\ y=(2)/(5)x+2\ is\ the\ required\ equation.}`

Answer 2

`y=(2)/(5)x+2`

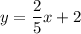
Explanation:

To determine the equation of the graphed line, first identify two points on the line:

• (-5, 0)
• (0, 2)

Substitute these points into the slope formula to find the slope (m) of the line:

`\textsf{Slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(2-0)/(0-(-5))=(2)/(5)`

The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.

The line crosses the y-axis at y = 2. Therefore, the y-intercept is 2.

Substitute the found slope and the y-intercept into the slope-intercept formula to create an equation of the graphed line:

`\boxed{y=(2)/(5)x+2}`