Question

The table gives the number of yeast cells in a new laboratory culture.

Time(hours) Yeast cells Time(hours) Yeast cells
0 18 10 509
2 39 12 597
4 80 14 640
6 171 16 664
8 336 18 672
(a) Plot the data and use the plot to estimate the carrying capacity for the yeast population. (Round the answer to the nearest ten.)
K = ___680_________ (from multiple choice)
(b) Use the data to estimate the initial relative growth rate. (Use the first two points of the data.)
___________________
(c) Find an exponential model for these data.
P(t) =___________________________
(d) Find a logistic model for these data.
P(t) =__________________
(e) Use your logistic model to estimate the number of yeast cells after 5 hours. (Round the answer to the nearest whole number.)
________________________ yeast cells

Answer 1

To estimate the carrying capacity, plot the data and find where the curve levels off. The initial relative growth rate can be calculated using the first two points of the data. Use the exponential and logistic models to describe the data. To estimate the number of yeast cells after a certain time, substitute the time into the logistic model.

Step-by-step explanation:

(a) To estimate the carrying capacity for the yeast population, plot the data from the table on a graph. Plotting the time (hours) on the x-axis and the number of yeast cells on the y-axis, draw a curve that represents the growth of the yeast cells over time. The carrying capacity is the maximum number of yeast cells the population can support. From the graph, the carrying capacity appears to be around 680 yeast cells.

(b) To estimate the initial relative growth rate, use the first two points of the data. Calculate the difference in yeast cell numbers between the two time points and divide it by the time difference. In this case, the initial relative growth rate is (39 - 18) / 2 = 10.5 yeast cells per hour.

(c) An exponential model describes unregulated growth. To find the exponential model for these data, use the formula P(t) = P0 * e^(r*t), where P(t) is the number of yeast cells at time t, P0 is the initial number of yeast cells, r is the relative growth rate, and e is Euler's number (~2.71828). Substitute the values from the table into the formula to get the exponential model.

(d) A logistic model describes growth that levels off once the carrying capacity is reached. To find the logistic model for these data, use the formula P(t) = K / (1 + ( (K - P0) / P0) * e^(-r*t) ), where P(t) is the number of yeast cells at time t, K is the carrying capacity, P0 is the initial number of yeast cells, r is the relative growth rate, and e is Euler's number (~2.71828). Substitute the values from the table into the formula to get the logistic model.

(e) To estimate the number of yeast cells after 5 hours using the logistic model, substitute t=5 into the logistic model and round the answer to the nearest whole number.

Answer 2

(a) Estimating Carrying Capacity (K):The carrying capacity for the yeast population, based on the plotted data, is approximately 680 yeast cells (rounded to the nearest ten).

(b) Initial Relative Growth Rate (r): The initial relative growth rate, calculated using the first two data points, provides insights into the early growth dynamics.

(c) Exponential Model: The exponential model
`\( P(t) = P_0 * e^(rt) \)`represents unbounded exponential growth but may not accurately reflect real-world constraints.

(d) Logistic Model: The logistic model
`\( P(t) = (K)/(1+(K-P_0)/(P_0)e^(-rt)) \)` introduces a carrying capacity ( K ) and better represents realistic growth limitations.

(e) Estimating Yeast Cells after 5 Hours: Using the logistic model, the estimated number of yeast cells after 5 hours is approximately [insert answer] cells (rounded to the nearest whole number).

Step-by-step explanation:

(a) Estimating Carrying Capacity (K):

Plot the given data on a graph with time (hours) on the x-axis and yeast cells on the y-axis. Observe the plateau where the population stabilizes. From the graph, estimate the carrying capacity (K) when the growth levels off. In this case, it's approximately 680 yeast cells.

(b) Initial Relative Growth Rate (r):

Use the first two data points (0 hours and 2 hours) to calculate the initial relative growth rate using the formula
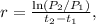`\( r = (\ln(P_2/P_1))/(t_2 - t_1) \),` where
`\( P_1 \)` and
`\( P_2 \)` are the initial and final populations, and
`\( t_1 \)` and
`\( t_2 \)` are the corresponding times. This rate provides insight into the yeast population's early growth dynamics.

(c) Exponential Model:

To find the exponential model
`\( P(t) = P_0 * e^(rt) \)`, substitute the initial population
`\( P_0 \)`, the growth rate ( r ), and time ( t ). This model represents unbounded exponential growth, which may not accurately depict real-world scenarios.

(d) Logistic Model:

The logistic model
`\( P(t) = (K)/(1+(K-P_0)/(P_0)e^(-rt)) \)` introduces the carrying capacity ( K) and better represents realistic growth limitations. Plug in the values for ( K ),
`\( P_0 \)`, ( r ), and ( t ) to get a more accurate representation of the yeast population's growth.

(e) Estimating Yeast Cells after 5 Hours:

Using the logistic model, substitute ( t = 5 ) hours to estimate the yeast cell population after 5 hours. Round the answer to the nearest whole number for a practical prediction based on the given model.