Question

Find the volume inside the paraboloid z = 9-x² - y², outside the cylinder x² + y² = 4, above the xy-plane.

Answer 1

Answer:
`(25\pi)/(2)`

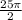
Explanation:

Detailed explanation is shown in the documents attached below. In part (1), we mainly discuss about how to get the limits of integration for variables r and
`\theta`, and transform the equation of paraboloid into polar form.

In part (2), we set up and evaluate the integral to determine the volume of the solid.

Answer 2

The paraboloid z = 9 - x² - y² and the cylinder x² + y² = 4 intersect when 9 - x² - y² = x² + y² = 4. Solving for x² and y², we get x² + y² = 2.5. This means the cylinder lies completely inside the paraboloid.

To find the volume between the paraboloid and cylinder, we can set up a triple integral in cylindrical coordinates:

V = ∫∫∫ dV = ∫∫∫ r dz dr dθ

The limits of integration are:

0 ≤ r ≤ √2.5, 0 ≤ θ ≤ 2π, and 4 - r² ≤ z ≤ 9 - r².

The bounds on z come from the equation of the paraboloid and the cylinder. We integrate with respect to z first:

∫∫∫ r dz dr dθ = ∫∫ (9 - r² - (4 - r²)) r dr dθ
= ∫∫ (5r - r³) dr dθ
= ∫ 0^{2π} ∫ 0^√2.5 (5r - r³) dr dθ
= ∫ 0^{2π} (5/2)r² - (1/4)r^4 |_0^√2.5 dθ
= ∫ 0^{2π} (5/2)(2.5) - (1/4)(2.5)² dθ
= ∫ 0^{2π} 10/2 dθ
= 5π

Therefore, the volume inside the paraboloid z = 9 - x² - y², outside the cylinder x² + y² = 4, above the xy-plane is 5π cubic units.