Hello !
Answer:
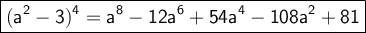
Explanation:
Let's use the binomial theorem to expand
 :
:
Binomial theorem :
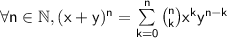
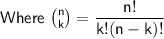
Reminders on factorials :
We have :
Now we substitute these values into the formula :
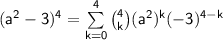
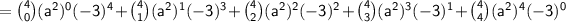
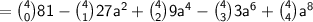
Let's calculate the binomial coefficients :
Now we can replace the binomial coefficients with their value:
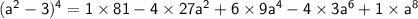
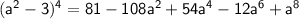
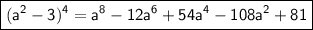
Have a nice day ;)