Question

NO LINKS!! URGENT HELP PLEASE!!!

Find the area of each figure. Round your answer to the nearest tenth.

Answer 1

3) 377.0 cm² (nearest tenth)

4) 14.5 yd² (nearest tenth)

Explanation:

To find the areas of the given regular polygons, first determine their side lengths and apothems, then use the area formula:

`\boxed{A=(n\cdot s\cdot a)/(2)}`

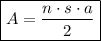
Question 3

The given diagram shows a ten-sided regular polygon with a side length measuring 7 cm. Therefore:

• Number of sides: n = 10
• Side length: s = 7

The formula for the apothem of a regular polygon is:

`\boxed{\begin{minipage}{5.5cm}\underline{Apothem of a regular polygon}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\where:\\\phantom{ww}$\bullet$ $s$ is the side length.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Therefore, to find an expression for the apothem, a, of the given regular polygon, substitute the values of s and n into the apothem formula:

`\implies a=(7)/(2 \tan\left((180^(\circ))/(10)\right))`

`\implies a=(7)/(2 \tan\left(18^(\circ)\right))`

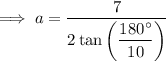
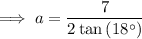
The formula for the area of a regular polygon is:

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=(n\cdot s\cdot a)/(2)$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}`

Therefore, to find the area of the given regular polygon, substitute the values of n, s and a into the area formula and solve for A:

`\implies A=(10 \cdot 7 \cdot (7)/(2 \tan\left(18^(\circ)\right)))/(2)`

`\implies A=(245)/(2\tan\left(18^(\circ)\right))}`

`\implies A=377.0\; \sf cm^2\;(nearest\;tenth)`

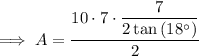
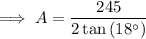
Therefore, the area of the given regular polygon is 377.0 cm² (nearest tenth).

`\hrulefill`

Question 4

The given diagram shows a seven-sided regular polygon with a side length measuring 2 yds. Therefore:

• Number of sides: n = 7
• Side length: s = 2

The formula for the apothem of a regular polygon is:

`\boxed{\begin{minipage}{5.5cm}\underline{Apothem of a regular polygon}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\where:\\\phantom{ww}$\bullet$ $s$ is the side length.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Therefore, to find an expression for the apothem, a, of the given regular polygon, substitute the values of s and n into the apothem formula and solve for a:

`\implies a=(2)/(2 \tan\left((180^(\circ))/(7)\right))`

`\implies a=(1)/( \tan\left((180^(\circ))/(7)\right))`

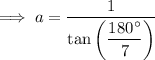
The formula for the area of a regular polygon is:

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=(n\cdot s\cdot a)/(2)$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}`

Therefore, to find the area of the given regular polygon, substitute the values of n, s and a into the area formula and solve for A:

`\implies A=(7\cdot 2\cdot (1)/( \tan\left((180^(\circ))/(7)\right)))/(2)`

`\implies A=(7)/( \tan\left((180^(\circ))/(7)\right))`

`\implies A=14.5\; \sf yd^2\;(nearest\;tenth)`

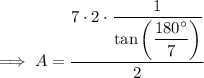
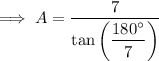
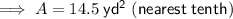
Therefore, the area of the given regular polygon is 14.5 yd² (nearest tenth).

Answer 2

3. 376.95cm^2

14. 14.5 yd^2

Explanation:

3.

no. of side (n)=10

length of one side(s)=7 cm

Perimeter(p)=n*s=10*7=70 cm

Now finding apothem(a),

`\bold{apothem(a)=(s)/(2Tan((180^o)/(n)))}`

by substituting value, we get,

`\bold{apothem(a)=(7)/(2Tan((180^o)/(10)))=10.77cm}`

Now, we have

`Area=(P*a)/(2)`

substituting value:

`Area=(70*10.77)/(2)=\bold{376.95 cm^2}`

`\hrulefill`

4.

no. of side (n)=7

length of one side(s)=2 yd

Perimeter(p)=n*s=7*2=14 cm

Now finding apothem(a),

`\bold{apothem(a)=(s)/(2Tan((180^o)/(n)))}`

by substituting value, we get,

`\bold{apothem(a)=(2)/(2Tan((180^o)/(7)))=2.076yd}`

Now, we have

`Area=(P*a)/(2)`

substituting value:

`Area=(14*2.076)/(2)=\bold{14.5yd^2}`

`\hrulefill`