Question

Line l bisects segment BC of triangle ABC, where A is at (3, -3), B is at (1, 4), and C is at (3, -2). If line l also travels through point A, what is its equation?

A. y=-5x-1
B. y=-2x+4
C. y=-4x+9
D. y=4x-1
E. y=5x+4

Answer 1

Option C y = -4x + 9

Explanation:

Equation of a line:

The line l bisects BC. The line l passes through the midpoint of BC.

B(1, 4) ; C(3 , -2)

`\sf Midpoint \ of \ BC = \left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`\sf = \left((1+3)/(2),\frac{4-2}2{}\right)\\\\\\=\left((4)/(2),(2)/(2)\right)\\\\\\=(2 , 1)`

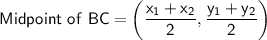
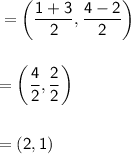
Line l passes through (2,1) and A(3 , -3),

`\sf \boxed{Slope =(y_2-y_1)/(x_2-x_1)}`

`\sf =(-3-1)/(3-2)\\\\\\=(-4)/(1)\\\\=-4`

m = -4

Equation of line in slope intercept form: y =mx +c

Here, m is the slope and c is the y-intercept.

y = -4x + c

As the line l is passing through (2,1), substitute the point (2,1) in the above equation and find c.

1 = -4*2 + c

1 = -8 + c

1 + 8 = c

c = 9

Equation of the line l:

y = -4x + 9