Question

NO LINKS!! URGENT HELP PLEASE!!

1. Find the area of a regular octagon. Each side is 12 m.

2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.

3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.

Answer 1

1.695.29 m^2

2.8 feet

3. 172.0477 in^2

Explanation:

1. The area of a regular octagon can be found using the formula:

`\boxed{\bold{Area = 2a^2(1 + √(2))}}`

where a is the length of one side of the octagon.

In this case, a = 12 m, so the area is:

`\bold{Area = 2(12 m)^2(1 + √(2)) = 288m^2(1 + \sqrt2)=695.29 m^2}`

Therefore, the Area of a regular octagon is 695.29 m^2

2.

The formula for the exterior angle of a regular polygon is:

`\boxed{\bold{Exterior \:angle = (360^o)/(n)}}`

where n is the number of sides in the polygon.

In this case, the exterior angle is 40°, so we can set up the following equation:

`\bold{40^o=( 360^0 )/(n)}`

`n=(360)/(40)=9`

Therefore, the polygon has n=9 sides.

Perimeter=72ft.

We have

`\boxed{\bold{Perimeter = n*s}}`

where n is the number of sides in the polygon and s is the length of one side.

Substituting Value.

72 feet = 9*s

`\bold{s =( 72 \:feet )/( 9)}`

s = 8 feet

Therefore, the length of each side of the polygon is 8 feet.

3.

Solution:

A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length =
`\bold{(perimeter)/(n)=(50)/(5 )= 10 in.}`

The area of a regular pentagon can be found using the following formula:

`\boxed{\bold{Area = (1)/(4)\sqrt{5(5+2√(5))} *s^2}}`

where s is the length of one side of the Pentagon.

In this case, s = 10 in, so the area is:

`\bold{Area= (1)/(4)\sqrt{5(5+2√(5))} *10^2=172.0477 in^2}`

Drawing: Attachment

Answer 2

1) 695.3 m²

2) 8 ft

3) 172.0 in²

Explanation:

Question 1

To find the area of a regular polygon, we can use the following formula:

`\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=(s^2n)/(4 \tan\left((180^(\circ))/(n)\right))$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}`

Given the polygon is an octagon, n = 8.

Given each side measures 12 m, s = 12.

Substitute the values of n and s into the formula for area and solve for A:

`\implies A=((12)^2 \cdot 8)/(4 \tan\left((180^(\circ))/(8)\right))`

`\implies A=(144 \cdot 8)/(4 \tan\left(22.5^(\circ)\right))`

`\implies A=(1152)/(4 \tan\left(22.5^(\circ)\right))`

`\implies A=(288)/(\tan\left(22.5^(\circ)\right))`

`\implies A=695.29350...`

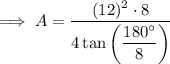
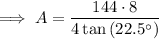
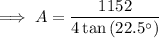
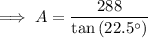
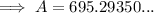
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.

`\hrulefill`

Question 2

The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.

If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.

To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:

`\boxed{\textsf{Interior angle of a regular polygon} = (180^(\circ)(n-2))/(n)}`

Therefore:

`\implies 140^(\circ)=(180^(\circ)(n-2))/(n)`

`\implies 140^(\circ)n=180^(\circ)n - 360^(\circ)`

`\implies 40^(\circ)n=360^(\circ)`

`\implies n=(360^(\circ))/(40^(\circ))`

`\implies n=9`

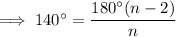
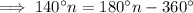
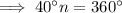
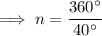
Therefore, the regular polygon has 9 sides.

To determine the length of each side, divide the given perimeter by the number of sides:

`\implies \sf Side\;length=\frac{Perimeter}{\textsf{$n$}}`

`\implies \sf Side \;length=(72)/(9)`

`\implies \sf Side \;length=8\;ft`

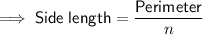
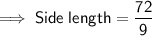
Therefore, the length of each side of the regular polygon is 8 ft.

`\hrulefill`

Question 3

The area of a regular polygon can be calculated using the following formula:

`\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=(s^2n)/(4 \tan\left((180^(\circ))/(n)\right))$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}`

A regular pentagon has 5 sides, so n = 5.

If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.

Substitute the values of s and n into the formula and solve for A:

`\implies A=((10)^2 \cdot 5)/(4 \tan\left((180^(\circ))/(5)\right))`

`\implies A=(100 \cdot 5)/(4 \tan\left(36^(\circ)\right))`

`\implies A=(500)/(4 \tan\left(36^(\circ)\right))`

`\implies A=(125)/(\tan\left(36^(\circ)\right))`

`\implies A=172.047740...`

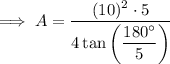
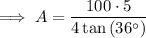
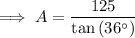
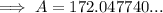
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.