Answer:
d) 171.8°
e) 72
f) 60°
Explanation:
Part d
The Polygon Interior Angle Theorem states that measure of the interior angle of a regular polygon with n sides is [(n - 2) · 180°] / 2.
The number of sides of a 44-gon is n = 44. Therefore, the measure of its interior angle is:
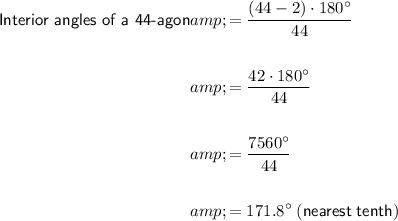
Therefore, the interior angle of a 44-gon is 171.8°.

Part e
The Polygon Interior Angle Theorem states that measure of the interior angle of a regular polygon with n sides is [(n - 2) · 180°] / 2.
Given the interior angle of a regular polygon is 175°, then:
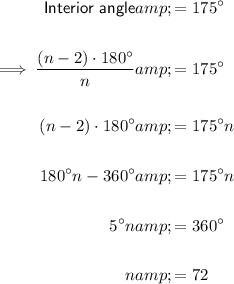
Therefore, the number of sides of the regular polygon is 72.

Part f
According the the Polygon Exterior Angles Theorem, the sum of the measures of the exterior angles of a polygon is 360°.
Therefore, to find exterior angle of a regular hexagon, divide 360° by the number of sides:

Therefore, the exterior angle of a regular hexagon is 60°.