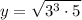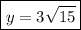Answer:
x = 3
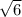
y = 3
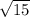
Explanation:
We know that when a right triangle is split at its altitude, all three resulting triangles are similar.
This means that we can equate the ratios of their side lengths.

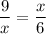
We can use this equation to solve for
 .
.
↓ multiplying both sides by

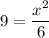
↓ multiplying both sides by 6
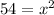
↓ taking the square root of both sides
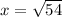
↓ simplifying the square root

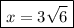
Now that we know what x is, we can solve for y using the Pythagorean Theorem.

↓ plugging in
 -value
-value
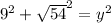
↓ simplifying exponents


↓ taking the square root of both sides
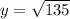
↓ simplifying the square root