Question

100 Points! Algebra question. Photo attached. Please show as much work as possible. Thank you!

Answer 1

Answer: sin 0 = sqrt(1 - (5/13)^2) = 12/13

Explanation:

A. Using the Pythagorean identity, we know that sin^2(0) + cos^2(0) = 1. Therefore, sin^2(0) + (5/13)^2 = 1. Solving for sin 0, we get:

sin 0 = ±sqrt(1 - (5/13)^2)

Since 0° < 0 < 90°, sin 0 must be positive.

Answer 2

`\sin(\theta) = (12)/(13)`

Explanation:

We know that the trigonometric ratio cosine is defined as:

`\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}`

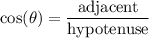
Therefore, from the given equation:

`\cos(\theta) = (5)/(13)`

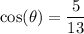
we can identify the following values:

`\text{adjacent} = 5`

`\text{hypotenuse} = 13`

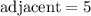
Since we know two sides of the right triangle which the cosine ratio is from, we can solve for the third side, opposite, using the Pythagorean Theorem.

`a^2 + b^2 = c^2`

↓ plugging in the adjacent and hypotenuse values

`5^2 + b^2 = 13^2`

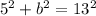
↓ simplifying the exponents

`25 + b^2 = 169`

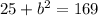
↓ subtracting 25 from both sides

`b^2 = 144`

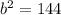
↓ taking the square root of both sides

`b = 12`

So, we know that
`\text{opposite} = 12`.

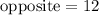Using this opposite value, we can solve for the trigonometric ratio sine.

`\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}`

`\boxed{\sin(\theta) = (12)/(13)}`