Question

Write the equation of the circle for which ý(22, 21) and p(6, 23) are the endpoints of

a diameter of the circle.

Answer 1

`(x-14)^2 +(y-22)^2 = (√(65))^2`

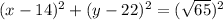
Explanation:

If the two given points are the extremes of the diameter, the center of the circle has to be its middle point - that we can find by taking the average of the coordinates. The center thus sits in

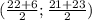`(\frac{22+6}2; \frac{21+23}2)` or
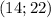`(14; 22)`. At this point we either find the length of the diameter and halve it, or the distance between the center and either point. Let's go for the diameter.

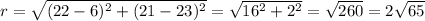`r=√((22-6)^2+(21-23)^2)=√(16^2+2^2) = \sqrt {260}=2√(65)`. That makes our radius half of that. We can easily write the equation of the circle now:

`(x-14)^2 +(y-22)^2 = (√(65))^2`

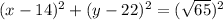
Now, in theory you can improve it by multiplying it out and taking every term to the LHS, but I think it's good enough like that.