Question

How long would it take for an investment of $1000 to double in value if it earns 5% compounded weekly? (Note: Write an equation to solve this problem, but solve the equation graphically, not algebraically.)

Answer 1

`\displaystyle 2000=1000\biggr(1+(0.05)/(52)\biggr)^(52t)`

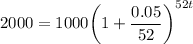
Explanation:

Recall the formula for compound interest is
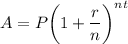`\displaystyle A=P\biggr(1+(r)/(n)\biggr)^(nt)` where
`P` is the principal/initial value,
`r` is the annual interest rate,
`n` is the number of times the interest is compounded, and
`t` is time in years.

Given there are 52 weeks in a year, and the annual interest rate is 5%, then
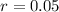`r=0.05` and
`n=52`. Thus, the equation would be:

`\displaystyle A=P\biggr(1+(r)/(n)\biggr)^(nt)\\\\\displaystyle 2P=P\biggr(1+(0.05)/(52)\biggr)^(52t)\\\\2(1000)=1000\biggr(1+(0.05)/(52)\biggr)^(52t)\\\\2000=1000\biggr(1+(0.05)/(52)\biggr)^(52t)`

2P is there because we want to have our initial value doubled by the end of the period.

Hope this helped!