Question

Find the area of a regular dodecagon (12 -gon) with a

side length of 9 inches. Round your answer to the
nearest hundredth.
The area is about
square inches.

Answer 1

906.89 in²

Explanation:

A regular dodecagon is a specific type of 12-sided polygon where all sides and angles are equal.

The formula for the area of a regular polygon is:

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=(n\cdot s\cdot a)/(2)$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}`

We know that the number of sides is 12 and that the length of one side is 9 inches, so in order to calculate the area, we first need to find the apothem.

The formula for the apothem of a regular polygon is:

`\boxed{\begin{minipage}{6cm}\underline{Length of apothem}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\\\where:\\\phantom{ww}$\bullet$ $a$ is the apothem.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Substitute s = 9 and n = 12 into the apothem formula, and solve for a:

`a=(9)/(2 \tan\left((180^(\circ))/(12)\right))`

`a=(9)/(2 \tan\left(15^(\circ)\right))`

`a=(9)/(2 \left(2-√(3)\right))`

`a=(9)/(4-2√(3))`

`a=(9)/(4-2√(3))\cdot (4+2√(3))/(4+2√(3))`

`a=(36+18√(3))/(4)`

`a=(18+9√(3))/(2)`

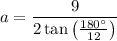
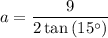
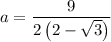
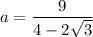
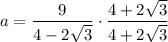
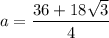
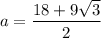
Now we have calculated the apothem, substitute this along with n = 12 and s = 9 into the area of a polygon formula

`A=(n \cdot s \cdot a)/(2)`

`A=(12 \cdot 9 \cdot (18+9√(3))/(2))/(2)`

`A=(108 \cdot (18+9√(3))/(2))/(2)`

`A=54 \cdot (18+9√(3))/(2)}`

`A=27\cdot (18+9√(3)})`

`A=486+243√(3)`

`A=906.89\; \sf in^2\;(nearest\;hundredth)`

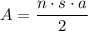
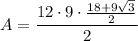
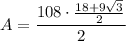
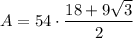
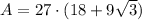
Therefore, the area of a regular dodecagon with a side length of 9 inches is 906.89 in² (nearest hundredth).

Note: Please see the attached image for confirmation of the area using a graphic calculator.