Question

How do you find cot Thea = 0 on unit circle

I don’t understand how to find cot(Thea)=0 on the unit circle and also cot(Thea)=-1

Answer 1

See below for explanation.

Explanation:

Each (x, y) point on the unit circle is equal to (cos θ, sin θ).

To find cot θ, where θ is the angle corresponding to the point (x, y) on the unit circle, we can use the formula:

`\boxed{\cot \theta=(\cos \theta)/(\sin \theta)=(x)/(y)}`

`\hrulefill`

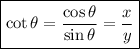
If cot θ = 0, then x must be zero. (If y was zero, the value would be undefined). Therefore, we need to find the points on the unit circle where the x-coordinate (cos θ) is zero.

The points on the unit circle where x = 0 are:

• (0, 1) and (0, -1)

The corresponding angles (in radians) at these points are:

`\bullet \quad (\pi)/(2)\;\;\textsf{and}\;\;(3\pi)/(2)`

Therefore, the cotangent has the value of zero at π/2 and 3π/2.

`\hrulefill`

If we divide a number by the same (but negative) number, we get -1.

Similarly, if we divide a negative number by the same (but positive) number, we get -1.

Therefore, if cot θ = -1, then the x-coordinate and y-coordinate of the points must be the same, but opposite signs.

The points on the unit circle where -x = y and x = -y are:

`\bullet \quad \left(-(√(2))/(2),(√(2))/(2)\right)\;\; \textsf{and}\;\;\left((√(2))/(2),-(√(2))/(2)\right)`

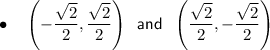
The corresponding angles (in radians) at these points are:

`\bullet \quad (3\pi)/(4)\;\;\textsf{and}\;\;(7\pi)/(4)`

Therefore, the cotangent has the value of -1 at 3π/4 and 7π/4.