Question

Find the average value of f(x) = √81 -x² over the interval [0, 9].

Answer 1

`f_(ave)=(9\pi)/(4)`

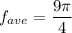
Explanation:

You want the average value of f(x) = √(81 -x²) on the interval [0, 9].

Area

The function f(x) defines a quarter circle of radius 9 in the first quadrant on the given interval. Its area is given by the formula in the problem statement:

A = (1/4)πr² = (π/4)·81

Average value

The average value of the function is the area divided by the width of the interval:

`f_(ave)=((81\pi)/(4))/(9)\\\\\\\boxed{f_(ave)=(9\pi)/(4)}`

__

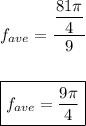
Additional comment

You will notice that the average value is π/4 times the radius. This is also true for a semicircle. The attachment shows the rectangle with area equal to that of the quarter circle.

<95141404393>