Question

For what values of m the equations mx-1000=1017 and 1017=m-1000x have a common root. PLSSS ANSWER!!!

Answer 1

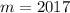`m = 2017` and
`m = -1000`

Explanation:

Given equations are (I am hoping it is 1017 as written by you)

From the first equation we get

`mx-1000=1017 \\\\\rightarrow mx = 1017 + 1000\\\\\rightarrow mx = 2017\\\\\rightarrow m = 2017/x\dots [1]`

From the second equation we get

`1017=m-1000x\\\\m-1000x = 1017\\\\m = 1000x + 1017 \dots[2]`

Equating [1] and [2] we get

`(2017)/(x) = 1000x + 1017\\\\`

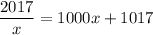
Multiply above equation throughout by x to get

`2017 = 1000x^2+ 1017x\\`

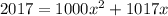
Subtract 2017 from both sides:
0 = 1000x^2 + 1017x - 2017\\\\

Switching sides:

`1000x^2 + 1017x - 2017 = 0\\\\`

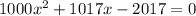
This is a quadratic equation in x which can be solved by the quadratic formula, completing the square or factorization

Let's choosing factoring to solve

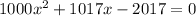`1000x^2 + 1017x - 2017 = 0` can be factored as

`\left(1000x^2-1000x\right)+\left(2017x-2017\right) = 0`\\\\

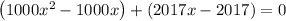Factor out 1000x from the first term and 2017 from the second term:

`\rightarrow 1000x(x - 1) + 2017(x -1) = 0`\\\\

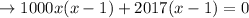Factor out common term x - 1:

`\left(x-1\right)\left(1000x+2017\right)\\\\`

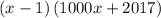
This means either
`x - 1 = 0 \;or\; 1000x + 2017 = 0`

giving two possible solutions

`x - 1 = 0 \rightarrow \boxed{x = 1}`

and

`1000x + 2017 = 0 \rightarrow 1000x = - 2017 \rightarrow \boxed{ x = -(2017)/(1000)}`

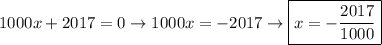
Use these two values of x in equation 1 to solve for possible values of m

At x = 1

`m = (2017)/(1) = 2017`

At

`x = -(2017)/(1000)`

`m = (2017)/(-(2017)/(1000))`

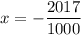
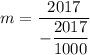
When dividing by a fraction, just multiply the numerator by the reciprocal of the denominator

`(a)/((b)/(c))=(a\cdot \:c)/(b)`

`m =(2017)/(-(2017)/(1000))\\\\\\= -(2017\cdot \:1000)/(2017)\\\\\\= - 1000`

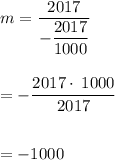
So the possible values of m are

`\text{m = 2017 \;and\; m = -1000}`