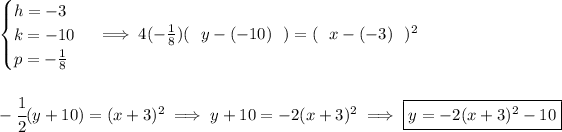Check the picture below.
so the parabola looks more or less like so, with a vertex at (-3 , 10) and the directrix above it at -79/8 or namely -9⅞, now, the directrix is just 1/8 of a unit above the vertex, that's our "p" distance, and since the directrix is above the vertex, the parabola is opening downwards and "p" is negative.
![\textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{p~is~negative}{op ens~\cap}\qquad \stackrel{p~is~positive}{op ens~\cup} \end{cases} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2024/formulas/mathematics/high-school/si7ghaijdnzfnyowi2bz3u4nzj6if41693.png)