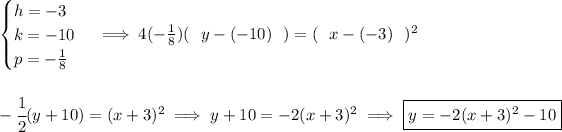Question

Vertex- (-3,-10)
Directrix- y=-79/8

Find the vertex form equation.

Answer 1

Check the picture below.

so the parabola looks more or less like so, with a vertex at (-3 , 10) and the directrix above it at -79/8 or namely -9⅞, now, the directrix is just 1/8 of a unit above the vertex, that's our "p" distance, and since the directrix is above the vertex, the parabola is opening downwards and "p" is negative.

`\textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{p~is~negative}{op ens~\cap}\qquad \stackrel{p~is~positive}{op ens~\cup} \end{cases} \\\\[-0.35em] ~\dotfill`

`\begin{cases} h=-3\\ k=-10\\ p=-(1)/(8) \end{cases}\implies 4(-(1)/(8))(~~y-(-10)~~) = (~~x-(-3)~~)^2 \\\\\\ -\cfrac{1}{2}(y+10)=(x+3)^2\implies y+10=-2(x+3)^2\implies \boxed{y=-2(x+3)^2-10}`