Final answer:
The remaining activity of the isotope ^85Sr in the patient's body after one year is approximately 1.42 μCi, computed using the half-life formula.
Step-by-step explanation:
To determine the remaining activity of the isotope ^85Sr in the patient's body after one year, we can use the concept of half-life. The half-life of ^85 Sr is 65 days, which means that every 65 days, the activity will reduce to half of its initial value.
The number of half-lives that have passed in one year (365 days) can be calculated as:
Number of half-lives = Total time elapsed / Half-life period
Number of half-lives = 365 days / 65 days = 5.615 (approximately)
To find the final activity after one year, we use the following formula:
Final activity = Initial activity x (1/2)^(Number of half-lives)
Plugging in the values:
Final activity = 0.10 mCi x (1/2)
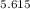
This results in a final activity of approximately 0.00142 mCi, which is equivalent to 1.42 μCi.