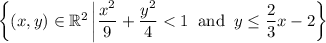F(x, y) = ln(36 − 4x^2-9y^2)+√(2x-3y-6) Find the domain of the function

Question

F(x, y) = ln(36 − 4x^2-9y^2)+
`√(2x-3y-6)`
Find the domain of the function

Answer 1

`\left\{(x,y) \in \mathbb{R}^2 \left|(x^2)/(9) + (y^2)/(4) < 1\;\;\text{and}\;\; y \leq (2)/(3)x - 2\right\}`

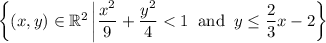
Explanation:

Given multivariable function:

`f(x,y)=\ln(36-4x^2-9y^2)+√(2x-3y-6)`

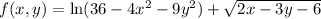
In order to determine the domain of the function, we need to find the values of x and y for which the function is defined and real.

The natural logarithm function ln(x) is defined only for positive real numbers, so we must have:

`36 - 4x^2 - 9y^2 > 0`

Simplify the inequality:

`4x^2 + 9y^2 < 36`

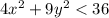
Divide both sides by 36:

`(x^2)/(9) + (y^2)/(4) < 1`

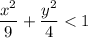
This is the equation of an ellipse centered at the origin with semi-axes of length 3 and 2 along the x and y directions, respectively. Therefore, the domain of the natural logarithm function is the interior of this ellipse.

The square root function is defined only for zero and positive real numbers:

`2x - 3y - 6 \geq 0`

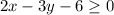
Simplifying to isolate y:

`2x - 3y \geq 6`

`(2)/(3)x - y \geq 2`

`y \leq (2)/(3)x - 2`

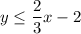
This is the equation of a line with slope 2/3 passing through the point (0, -2). The domain of the square root function is the set of points below this line, including the line itself.

Putting these conditions together, the domain of the function f(x,y) is the intersection of the interior of the ellipse and the region below the line.

Therefore, the domain can be written as:

`\left\{(x,y) \in \mathbb{R}^2 \left|(x^2)/(9) + (y^2)/(4) < 1\;\;\text{and}\;\; y \leq (2)/(3)x - 2\right\}`