Answer:
The volume of cone is 125600.
Step-by-step Step-by-step explanation :
GIVEN :
 Slant height of cone = 25
Slant height of cone = 25
 Radius of cone = 15
Radius of cone = 15
TO FIND :
 Volume of cone
Volume of cone
USING FORMULAS :

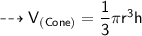
 l = slant height
l = slant height
 V = volume
V = volume
 π = 3.14
π = 3.14
 r = radius
r = radius
 h = height
h = height
SOLUTION :
Firstly, finding the height of cone by substituting all the given values in the formula :

Hence, the height of cone is 20.

Now, calculating the volume of cone by substituting all the given values in the formula :

Hence, the volume of cone is 125600.
————————————————