Question

Line e passes through points (5, 14) and (10, 6). Line f is perpendicular to e. What is the slope of line f?

Answer 1

Slope of line f: m = 5/8

Explanation:

Step 1: First, we need to find the slope (m) of line e using the slope formula, which is

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

• (x1, y1) is one point of the line and (x2, y2) is another point on the line
• We can allow (5, 14) to be our (x1, y1) point and (10, 6) to be out (x2, y2) point:

`m=(6-14)/(10-5)\\ \\m=-8/5`

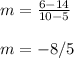
Step 2: We know that when two lines are perpendicular, their slopes are negative reciprocals. We can see this with the following formula:

`m_(2)=-(1)/(m_(1) )`,

• m2 is the slope of the line we're trying to find (slope of line f in this case)
• m1 is the slope of the line we're given or have found (slope of line e, namely -8/5)

m2 = -1 / (-8/5)

m2 = 5/8