Question

Describing a System of Two-Variable Inequalities

Which statements are true about the graph of y ≤ 3x + 1 and y2-x+ 2? Check all that apply.

The slope of one boundary line is 2.

Both boundary lines are solid.

A solution to the system is (1, 3).

Both inequalities are shaded below the boundary lines.

The boundary lines intersect.

Intro

4 [

7 of 10

Done

Answer 1

In a system of two-variable inequalities, the statements that are true about the given graph are the slope of one boundary line is 2, both boundary lines are solid, and the boundary lines intersect.

Step-by-step explanation:

In the given system of two-variable inequalities, y ≤ 3x + 1 and y2-x+ 2, the statements that are true are:

• The slope of one boundary line is 2.
• Both boundary lines are solid.
• The boundary lines intersect.

A solution to the system is not specified in the question, so we cannot determine whether (1,3) is a solution or not. Additionally, it is not mentioned whether both inequalities are shaded below the boundary lines, so we cannot determine the accuracy of that statement either.

Answer 2

The following statements are True: Both boundary lines are solid, A solution to the system is (1, 3) and The boundary lines intersect.

To determine which statements are true about the graph of the system of inequalities
`\[y \leq 3x + 1\]` and
`\[y \geq -x + 2\]`, let's analyze each statement one by one.

1. The slope of one boundary line is 2:
To determine if this statement is true, we must look at the slopes of the boundary lines of each inequality. The slope-intercept form of a line is given by y = mx + b, where m is the slope and b is the y-intercept. In the inequality
`\[y \leq 3x + 1\]`, the slope of the boundary line is 3. For the second inequality
`\[y \geq -x + 2\]`, the slope of the boundary line is -1. Neither boundary line has a slope of 2, so this statement is False.

2. Both boundary lines are solid:
When an inequality is inclusive, which is indicated by
`\(\leq\) or \(\geq\)`, the boundary line is drawn as a solid line on the graph. Since both inequalities
`\(y \leq 3x + 1\) and \(y \geq -x + 2\)` are inclusive (as indicated by the
`\(\leq\) and \(\geq\)`), both boundary lines are indeed solid. This statement is True.

3. A solution to the system is (1, 3):
To determine if a given point is a solution to the system, we plug the values into both inequalities. For the point (1, 3), let's substitute x with 1 and y with 3:

For
`\(y \leq 3x + 1\):`

`\[3 \leq 3(1) + 1\]`

`\[3 \leq 3 + 1\]`

`\[3 \leq 4\]` (True)

For
`\(y \geq -x + 2\)`:

`\[3 \geq -1(1) + 2\]`

`\[3 \geq -1 + 2\]`

`\[3 \geq 1\]` (True)

Since (1, 3) satisfies both inequalities, this statement is True.

4. Both inequalities are shaded below the boundary lines:
When we shade the graph of an inequality, we shade below the line if the inequality is
`\(\leq\)` and above the line if it is
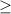`\(\geq\)`. For the first inequality
`\(y \leq 3x + 1\)`, we would indeed shade below the boundary line. However, for the second inequality
`\(y \geq -x + 2\)`, we would shade above the boundary line. Therefore, not both inequalities are shaded below their respective boundary lines, making this statement False.

5. The boundary lines intersect:
If two boundary lines have different slopes, they must intersect at some point unless they are vertical or horizontal lines that run parallel to the axes. Since the slopes of the boundary lines are 3 and -1, they are different and not parallel to any axis. Thus, the boundary lines must intersect somewhere on the graph. This statement is True.

Question:
Which statements are true about the graph of
`y \leq 3x + 1` and
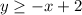`y \geq -x + 2`? Check all that apply.

O The slope of one boundary line is 2.

O Both boundary lines are solid.

O A solution to the system is (1, 3).

O Both inequalities are shaded below the boundary lines

O The boundary lines intersect.