Question

king kong leaned his 65 body against the empire state building. His feet were 25 from the base of the building. How far up the side of the building did his head touch?

Answer 1

He will connect with the building 60 units from the ground.

Explanation:

Main concepts:

Concept 1. Visualizing the scenario

Concept 2. Setting up the equation for a right triangle

Concept 3. Solving for an unknown variable in a one-variable equation

Concept 4. Simplifying a radical

Concept 1. Visualizing the scenario

If King Kong is 65 units tall, and he is 25 units away leaning against a building, then he is not just like standing right next to a wall and leaning against it, but he is very tilted at an angle.

The building, as with nearly every building can be assumed to form a right angle (90 degrees) with the ground, and thus King Kong, the portion of the ground between the building and King Kong's feet, and the portion of the building from the ground to King Kong's head, will form the three sides of a right triangle.

Since the building and the ground form are the sides that form a right angle, King Kong forms the side across from the right angle and his height (albeit tilted diagonally) is the hypotenuse.

Concept 2. Setting up the equation for a right triangle

For any right triangle, the length of the sides of the right triangle obey the equation:
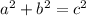`a^(2) +b^(2) =c^(2)` where c is the hypotenuse, and a & b are the legs (the other two sides that form the right angle) of the right triangle.

Side note: Due to the commutative property of addition, a & b are interchangeable, and either a or b could be used for the height of point where he connects with the building or the distance along the ground between the building and his feet. For ease of remembering what represented what, we'll choose "b" to be the "distance along the ground" which I'm visualizing as the "base" of the triangle.

Since King Kong's height (the hypotenuse, c) is known, and the distance along the ground (b) is known, we can substitute the known values into the equation, and solve for the unknown value (a) representing the distance requested in the question.

`a^(2) +b^(2) =c^(2)`

`a^(2) +(25)^(2) =(65)^(2)`

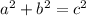
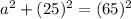
First, simplify the expressions of numbers squared...

25 squared is 25*25, which equals 625.

65 squared is 65*65, which equals 4225.

`a^(2) +625 =4225`

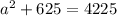
Concept 3. Solving for an unknown variable in a one-variable equation

To solve for "a", we'll need to undo the things connected to it. "a" exists only once on the left side of the equation. Focusing only on the left side, some things were done to "a" do make it equal the right side. Order of operations would first square "a" (do the exponent first), and then add 625.

To undo multiple steps, we'll need to undo them in reverse order.

So, we'll need for first undo adding by 625, then undo squaring.

To undo addition, we'll apply the opposite operation (subtraction) by subtracting 625 from both sides of the equation:

`(a^(2) +625)-625 =(4225)-625`

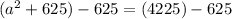
Notice how on the left hand side of the equation, the "a-squared" first adds 625, then subtracts 625. That won't change the value and it will remain "a-squared"

`a^(2)=(4225)-625`

On the right hand side, 4225 minus 625 is 3600

`a^(2)=3600`

Next, to undo an exponent, we need to do the opposite (use a radical). The index of the radical should match the exponent, so if the exponent were a "5", we'd want the fifth root to undo it.

In this case, we want a 2nd root (most commonly called a square root).*

*Officially, to undo an even exponent, we have to apply a "square root rule", which gives two answers, a positive and a negative answer with the same magnitude. However, we know that "how far up the side of the building" is not a negative number, so we can ignore that here.

`\sqrt{a^(2)}=√(3600)`

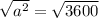
Again, the radical and the exponent undo each other, because taking whatever number "a" is and squaring it, and then immediately taking the square root, will just arrive back at the value you started with, "a".

`a=√(3600)`

Concept 4. Simplifying a radical

On the right hand side of the equation, to simplify radicals by hand, factor the number inside the radical, and form groups of matching numbers where the group size is the index of the radical. In this case, the index is "2", so pairs of numbers that match.

3600=

=36*100

=(6*6)*(10*10)

Often, the number will be factored all the way down to prime numbers, but if you've found a group that matches, it can be factored out of the radical (only bring out one number from each group to represent the group).

If everything factors out, it was a perfect "index" number (in this case, a perfect square number). If this happens, there is no radical left over at the end, and all of the numbers that were factored out, multiply together to make the answer.

`a=6*10`

`a=60`

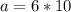
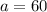
This result can be verified by calculator: the square root of 3600 is 60.

So, if King Kong is 65 units tall, and leans against he building with his feet 25 units away, he will connect with the building 60 units from the ground.