A rule that describes the piecewise-defined function in the graph above include the following: B.
 .
.
A piecewise-defined function is a type of function that is defined by two or more mathematical expressions over a specific domain.
Note: The inequality symbol < or > represents a hollow dot (circle).
The inequality symbol ≤ or ≥ represents a solid dot (circle).
Generally speaking, the domain of any piecewise-defined function is the union of all of its sub-domains. By critically observing the graph of this piecewise-defined function, we have the following functions;
Over the interval x < -2, a downward sloping lineextends infinitely to the left and must be denoted by this function;
g(x) = -1/2(x) + 1, when x < -2.
Over the interval -2 ≤ x < 0, a curve approaches the point (0, 6) and must be denoted by this function;
g(x) =
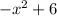 , when -2 ≤ x < 0.
, when -2 ≤ x < 0.
Over the interval 0 < x ≤ 4, a horizontal line approaches the point (4, 6) and must be denoted by this function;
g(x) = 6, when 0 < x ≤ 4.
Over the interval x > 4, a upward sloping line extends infinitely and must be denoted by this function;
g(x) = x + 2, when x > 4.