Question

2.

Graham wants to take snowboarding lessons at a nearby ski resort that charges $40 per week.
The resort also charges a one-time equipment-rental fee of $99 for uninterrupted enrollment in
classes. The resort requires that learners pay for three weeks of classes at a time.
The function f(x) represents the situation
f(x) =
40x +99
x
Select two choices that are true about the function f(x).
A There is a zero at 0.
B There is an asymptote at y = 40.
C
There is an asymptote at x = 0.
D There is a vertical shift up 99 units.

Answer 1

Options B & C

There is an asymptote at y = 40.

There is an asymptote at x = 0.

Explanation:

Main concepts:

Concept 1. Zeros of rational functions

Concept 2. Vertical asymptotes of rational functions

Concept 3. Horizontal asymptotes of rational functions

Concept 4. Transformations - vertical shift

Concept 1. Zeros of rational functions

Rational functions have zeros at values of x where the numerator is zero, while the denominator is not also zero.

`f(x)=(40x+99)/(x)`

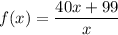
Values that make the denominator zero
Note that for the function f(x), x=0 is the only value that will make the denominator zero.

Values that make the numerator zero
To find the value that makes the numerator zero, set the numerator equal to zero, and solve for the value of x that makes it true:

`40x+99=0`

`40x=-99`

`x=(-99)/(40)`

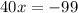
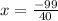
So,
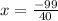`x=(-99)/(40)` is the only value that will make the numerator zero

Note that this doesn't simultaneously make the denominator zero, so
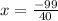`x=(-99)/(40)` is a zero (and the only zero) of the function f(x).

Therefore, Option A is NOT a correct answer.

Concept 2. Horizontal asymptotes of rational functions

Rational functions have Horizontal Asymptotes if the degree of the polynomial in the numerator is less than or equal to the degree of the polynomial in the denominator.

If the Degree of the denominator is greater, the Horizontal Asymptote is at a y=0.

If the Degrees are equal, the Horizontal Asymptote is at a y-value equal to the ratio of the leading coefficients.

`f(x)=(40x+99)/(x)`

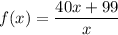
Note that for f(x), the degrees of the polynomials in the numerator and denominator are both 1. So, a horizontal asymptote does exist, and it is at a height of the ratio of the leading coefficients.

The leading coefficient of the numerator is 40, while the leading coefficient of the denominator is 1.

The ratio of the leading coefficients, 40/1, so the horizontal asymptote is y=40.

Therefore, Option B is a correct answer choice.

Concept 3. Vertical asymptotes of rational functions

Rational functions have Vertical Asymptotes at values of x where the denominator is zero, while the numerator is not also zero (the opposite of finding "zeros" of the function).

Recalling the values that make the numerator and denominator zero from Concept 1:

• x=0 is the only value that will make the denominator zero
• 
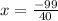  `x=(-99)/(40)` is the only value that will make the numerator zero

Since x=0 doesn't also make the numerator zero, x=0 is a vertical asymptote for the function f(x).

Therefore, Option C is a correct answer choice.

Concept 4. Transformations - vertical shift

Rational functions have been vertically shifted if after all the main rational function fraction, there is a number added or subtracted.

I provide an example of a different function (which I'll call g(x)) here:

`g(x)=(3)/(x)+2`

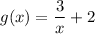
Observe that the "+2" is after all of the main fraction, so the graph of 3/x would have been shifted vertically up 2 units.

This is NOT the case for the function f(x) from the question. The "99" is part of the fraction, so it does not represent a vertical shift.

Therefore, Option D is NOT a correct answer choice.