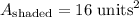Answer:
The total area of the shaded region is 16 square units
Explanation:
Main Steps:
Step 1. Find length of Square edge & Equilateral triangle leg
Step 2. Find the length from top to bottom of the full diamond
Step 3. Find the Area of the full diamond
Step 4. Find the Area that isn't shaded
Step 5. Find the Area that is shaded
Step 1. Find length of Square edge & Equilateral triangle edge
Since the Square has an area of 16 square units, using the formula for area of a square, the edge length must be 4 units
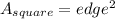
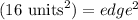
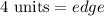 of square
of square
Since one edge of the equilateral triangle shares one edge of the square, they are the same length. Thus, the equilateral triangle also has edge length of 4 units.
Step 2. Find the length from top to bottom of the full diamond
Equilateral triangles have a height that is exactly
 the length of their base. So the height of the equilateral triangle is
the length of their base. So the height of the equilateral triangle is
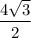 , or more simply
, or more simply
 .
.
The full diamond, from top to bottom, is the height of two of those equilateral triangles, plus the height of the central square:

Combining like terms, the length of the Diamond diagonal from top to bottom is
 .
.
Note, that due to symmetry of construction, this is also the length of the diamond's diagonal from left to right.
Step 3. Find the Area of the full diamond
One fact from geometry is that the area of a rhombus (all side lengths congruent), is given by the following formula:
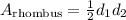 , where d1 and d2 are the lengths of the two diagonals.
, where d1 and d2 are the lengths of the two diagonals.
The "diamond" that was constructed, has all sides congruent (all sides the same length), so it is a rhombus (with matching diagonal lengths that we just calculated in Step 2)
Thus, the Area of the rhombus is:
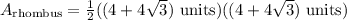
Using FOIL,
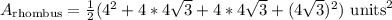
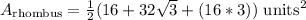
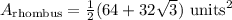
Distributing...
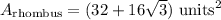
Step 4. Find the Area that isn't shaded
The area that isn't shaded is the area of the square, plus 4 equilateral triangles.
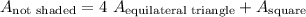
Recall that the area of a triangle is 1/2 * b * h
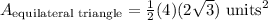
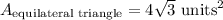
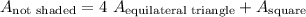

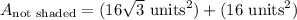
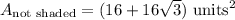
Step 5. Find the Area that is shaded
Lastly, the area that is shaded is the area of the full diamond/rhombus, minus the area that is not shaded:
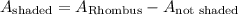
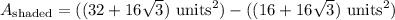
Combining like terms and simplifying...