Question

A ball is thrown with an initial velocity of 20 m/s at an angle of 60° above the horizontal. If we can neglect air resistance, what is the horizontal component of its instantaneous velocity at the exact top of its trajectory?.

Answer 1

`10\; {\rm m\cdot s^(-1)}`.

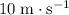Step-by-step explanation:

Under the assumption that air resistance on the ball is negligible, gravitational pull from the Earth would be the only force acting on the ball during the flight.

The resultant force on the ball would be equal to the gravitational pull, which is entirely in the vertical direction. Thus, the net force in the horizontal direction would be
`0` while the ball is in the air.

By Newton's Laws of Motion, since horizontal acceleration is
`0` during the flight, velocity of the ball in the horizontal direction would stay unchanged in a translational equilibrium.

It is given that the ball was launched at an angle of elevation of
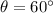`\theta = 60^(\circ)` above the horizon. The initial velocity
`u` of the ball can be decomposed into two components:

• Initial vertical velocity:
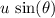  `u\, \sin(\theta)` (opposite to the angle of elevation,) and
• Initial horizontal velocity
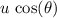  `u\, \cos(\theta)` (adjacent to the angle of elevation.)

With
`u = 20\; {\rm m\cdot s^(-1)}`, the horizontal velocity of the ball at launch would be
`(20\; {\rm m\cdot s^(-1)})\, \cos(60^(\circ)) = 10\; {\rm m\cdot s^(-1)}`.

Since the horizontal velocity of the ball stays unchanged during the flight, the horizontal velocity of the ball at the vertex of the trajectory would be equal to the value at launch:
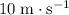`10\; {\rm m\cdot s^(-1)}`.