Question

Find the partial sum for the sequence.

{0, −1, −3, −6, −10, ...}; S14
S14=

Answer 1

`91`

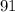
Explanation:

The partial sum of a sequence is the sum of a certain number of terms in the sequence. For the given sequence

{0, −1, −3, −6, −10, ...},

The nth term can be represented as Tn = n(n-1)/2. This means that the partial sum of the first 14 terms of the sequence, denoted by S14, can be calculated by adding up the first 14 terms using the formula: S14 = 0 + (-1) + (-3) + (-6) + (-10) + ... + T14.

Simplifying this expression using the formula for Tn, We get S14 = 91. Therefore, the partial sum for the given sequence up to the 14th term is equal to 91.

Answer 2

-91

Explanation:

To find the partial sum for the sequence

`\large \boxed{\mathrm{ \ 0, \ -1, \ -3, \ -6, \ -10,}}`

We first notice that the first term is

`\large \boxed{\mathrm{0}}`,

And each subsequent term is the sum of the previous term and the next integer in the sequence starting with
`-1.` Therefore, we can use the formula for the sum of an arithmetic series to find the partial sum S14:

S14 = 14/2 * (2(0) + (14-1)(-1+0)/2) = 14/2 * (13/2 * -1) = -91

Therefore, the partial sum for the sequence up to the
`14th` term is
`-91.`