Question

NO LINKS!!! URGENT HELP PLEASE!!!

Show that the triangle with vertices A, B, and C is a right triangle.

Answer 1

`\left[d(A,C)\right]^2=\boxed{178}`

`\left[d(A,B)\right]^2+\left[d(B,C)\right]^2=\boxed{128+50=178}`

`\text{Area of the triangle}=\boxed{40}\; \text{units}^2`

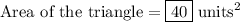
Explanation:

From inspection of the given triangle, the coordinates of vertices A, B and C are:

• A = (9, 4)
• B = (1, -4)
• C = (-4, 1)

We can use the distance formula to find the lengths of the sides of triangle ABC.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance between two points}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

`\begin{aligned}d(A, C) & =√((x_C-x_A)^2+(y_C-y_A)^2)\\& =√((-4-9)^2+(1-4)^2)\\& =√((-13)^2+(-3)^2)\\& =√(169+9)\\& =√(178)\end{aligned}`

`\begin{aligned}d(A, B) & =√((x_B-x_A)^2+(y_B-y_A)^2)\\& =√((1-9)^2+(-4-4)^2)\\& =√((-8)^2+(-8)^2)\\& =√(64+64)\\& =√(128)\end{aligned}`

`\begin{aligned}d(B, C) & =√((x_C-x_B)^2+(y_C-y_B)^2)\\& =√((-4-1)^2+(1-(-4))^2)\\& =√((-5)^2+(5)^2)\\& =√(25+25)\\& =√(50)\end{aligned}`

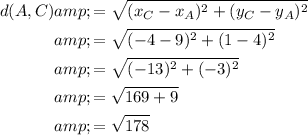
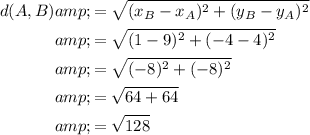
Pythagoras Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Therefore, to determine if triangle ABC is a right triangle, substitute the found side lengths into the Pythagoras Theorem:

`\begin{aligned}\implies \left[d(A, B)\right]^2 + \left[d(B, C)\right]^2 &= \left[d(A, C)\right]^2\\\left[√(128)\right]^2+\left[√(50)\right]^2&=\left[√(178)\right]^2\\128+50&=178\\178&=178\end{aligned}`

As the equation is true, this proves that triangle ABC is a right triangle.

The area of a right triangle is half the product of the lengths of its legs.

The legs of triangle ABC are AB and BC.

Therefore, the area of triangle ABC is:

`\begin{aligned}\text{Area\;of\;triangle\;$ABC$}&=(1)/(2) \cdot d(A,B) \cdot d(B,C)\\\\&=(1)/(2) \cdot √(128) \cdot √(50)\\\\&=(1)/(2) \cdot √(128 \cdot 50)\\\\&=(1)/(2) \cdot √(6400)\\\\&=(1)/(2) \cdot √(80^2)\\\\&=(1)/(2) \cdot 80\\\\&=40\; \text{square\;units}\end{aligned}`

Therefore, the area of the triangle is 40 square units.