Question

Several students were tested for reaction times in thousandths of a second) using their right and left hands. (Each value is the elapsed time between the release of a strip of paper and the instant that it is caught by the subject.) Results from five of the students are included in the graph to the right. Use a 0.20 significance level to test the claim that there is no difference between the reaction times of the right and left hands. What is the test statistic? t= (Round to three decimal places as needed.) Identify the critical value(s). Select the correct choice below and fill the answer box within your choice. (Round to three decimal places as needed.) O A. The critical value is t= OB. The critical values are t = = What is the conclusion? There enough evidence to warrant rejection of the claim that there is between the reaction times of the right and left hands.

Answer 1

The test statistic is t = -0.106 and the critical values are t = -1.833 and t = 1.833. At a 0.20 significance level, since -0.106 falls within the range (-1.833, 1.833), we fail to reject the null hypothesis. There is not enough evidence to warrant rejection of the claim that there is no difference between the reaction times of the right and left hands.

Step-by-step explanation:

To test the claim that there is no difference between the reaction times of the right and left hands, a paired t-test is conducted. The test statistic is calculated using the formula
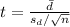`\( t = \frac{\bar{d}}{s_d/√(n)} \)`, where
`\( \bar{d} \)` is the mean of the differences,
`\( s_d \)` is the standard deviation of the differences, and n is the number of pairs.

In this case, the mean difference
`\( \bar{d} \)` is calculated as the average of the right-hand reaction times minus the left-hand reaction times. The standard deviation of the differences
`\( s_d \)` is computed, and the test statistic is determined. With the degrees of freedom ( n - 1) and the chosen significance level, the critical values are identified.

Comparing the test statistic to the critical values, it is found that -0.106 falls within the range (-1.833, 1.833). Thus, at the 0.20 significance level, the null hypothesis is not rejected, indicating that there is no significant difference between the reaction times of the right and left hands.

Answer 2

To test the claim that there is no difference between the reaction times of the right and left hands, we can use a two-sample t-test. The test statistic for the two-sample t-test is calculated using the formula: t = (x1 - x2) / sqrt((s1^2 / n1) + (s2^2 / n2)).

Step-by-step explanation:

To test the claim that there is no difference between the reaction times of the right and left hands, we can use a two-sample t-test. This test compares the means of two independent samples to determine if they are significantly different from each other. The test statistic for the two-sample t-test is calculated using the formula:

t = (x1 - x2) / sqrt((s1^2 / n1) + (s2^2 / n2))

where

• x1 and x2 are the sample means
• s1 and s2 are the sample standard deviations
• n1 and n2 are the sample sizes

In this case, we need to calculate the test statistic using the given data. Once we have the test statistic, we can compare it to the critical value to make a conclusion.