This can be solved for λ using numerical methods or by rearranging the terms and solving for λ algebraically. Once λ is found, we can use the expressions for x1, x2, and x3 to find the optimal consumption of each good.
To find the optimal consumption of X1, X2, and X3, we need to maximize utility subject to the budget constraint. Mathematically, this can be represented as:
Maximize U(x1, x2, x3) =
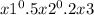
Subject to P1x1 + P2x2 + P3x3 = I
Taking the partial derivative of U with respect to each variable and setting them equal to λ (the Lagrange multiplier) times the partial derivative of the budget constraint with respect to the corresponding variable, we get:
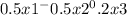 = λP1
= λP1
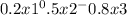 = λP2
= λP2
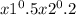 = λP3
= λP3
We can then solve this system of equations to find the optimal values of x1, x2, and x3. Here, we can use the third equation to express x2 in terms of x1 and substitute into the first two equations. This yields:
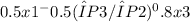 = λP1
= λP1
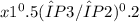 = λP3
= λP3
Simplifying and solving for x1, we get:
x1 =
![[(λP1)^2/(0.5λP3)(λP2)^0.8)]^2/3](https://img.qammunity.org/2024/formulas/business/high-school/9zk7u5z9u1z29rgdyr5qnuhi3pte16f1a1.png)
Using this value of x1, we can find x2 and x3:
x2 =

x3 = (I - P1x1 - P2x2)/P3
Overall, the optimal consumption of X1, X2, and X3 is given by:
x1 =
![[(λP1)^2/(0.5λP3)(λP2)^0.8)]^2/3](https://img.qammunity.org/2024/formulas/business/high-school/9zk7u5z9u1z29rgdyr5qnuhi3pte16f1a1.png)
x2 =

x3 = (I - P1x1 - P2x2)/P3
To solve for λ, we use the budget constraint:
P1x1 + P2x2 + P3x3 = I
Substituting in the expressions for x1, x2, and x3, we get:
![P1[(λP1)^2/(0.5λP3)(λP2)^0.8)]^2/3 + P2[(λP3/(λP2))^0.2 [(λP1)^2/(0.5λP3)](https://img.qammunity.org/2024/formulas/business/high-school/qe3kocbcv5b623rgc2awv019jhzlrpm5xd.png)
![(λP2)^0.8)]^0.5 + P3[(I - P1[(λP1)^2/(0.5λP3)(λP2)^0.8)]^2/3 -](https://img.qammunity.org/2024/formulas/business/high-school/aaystf8wu0871dos0adfz80n5gdcjt6y8s.png)
![P2[(λP3/(λP2))^0.2 [(λP1)^2/(0.5λP3)(λP2)^0.8)]^0.5]/P3](https://img.qammunity.org/2024/formulas/business/high-school/18kgzwup1q1zk4zktw5a51tdzmd4a04617.png) = I
= I